Last time we dug into random groups — MurphyKate’s favorite kind of group (until she heard my presentation on braids). We also covered the Gromov density model and small cancellation. Some of the key points picked up can be summed up in the following four theorems.
Theorem Small cancellation implies hyperbolicity
Theorem If the Gromov density ![]() implies small cancellation
implies small cancellation
Theorem If the Gromov density ![]() implies hyperbolicity
implies hyperbolicity
Theorem If the Gromov density ![]() implies hyperbolicity.
implies hyperbolicity.
Now that we have recalled all that fun stuff, let’s get on to business! It’s time for CAT(0) Cube Complexes (CCCs).
In essence, what we seek to achieve is a generalization of hyperbolicity. We have seen it in triangles and quadrilaterals, but how can we talk about hyperbolicity in ![]() -dimensions. What we seek to do is avoid positive curvature. In the Euclidean plane this means to avoid circles. Today, e will get closer to this idea and find what we need to avoid in
-dimensions. What we seek to do is avoid positive curvature. In the Euclidean plane this means to avoid circles. Today, e will get closer to this idea and find what we need to avoid in ![]() -dimensions. But first, a whole lot of definitions are needed…
-dimensions. But first, a whole lot of definitions are needed…
Definition A group is cubulated if it acts geometrically by isometries on a CCC.
This definition utterly meaningless — since we don’t know what a CCC is. The overall notion is that we want a group on which we can tile our cubes and cube complexes, which respects isometries, and behaves hyperbolically in ![]() -dimensions. Furthermore, we can fix that by actually defining what a CCC is, and for that matter what a cube complex is.
-dimensions. Furthermore, we can fix that by actually defining what a CCC is, and for that matter what a cube complex is.
Definition A cube complex is a space made by gluing together cubes along faces isometrically.
Now this, we can actually decipher. It is likely easiest to do so with a few drawn out examples. Here are some cube complexes:

And here is a NON cube complex:

A few notes we should make are that cube complexes can be infinite and furthermore can tile an ![]() -dimensional space!
-dimensional space!
Ok, great… but what was that CAT(0) part about. Well, we call a cube complex a CAT(0) cube complex if the cube complex has no corners unless they are “filled in” for dimension of ![]() . What we seek to do here isto avoid positive curvature. As with
. What we seek to do here isto avoid positive curvature. As with ![]() -slim triangles, we know that we are good with negative and flat curvature. However, when curvature turns positive and that is when hyperbolicity breaks. Thus it is useful to think of the CAT(0) condition as a requirement for a cube complex to be hyperbolic.
-slim triangles, we know that we are good with negative and flat curvature. However, when curvature turns positive and that is when hyperbolicity breaks. Thus it is useful to think of the CAT(0) condition as a requirement for a cube complex to be hyperbolic.
We have encountered CCCs before! In fact, every tree is a CCC. On the other hand, any graph which is not a tree is not a CCC. We won’t learn too many more details about cube complexes, but if you would like to learn more, this source should direct you to some wonderful ideas on low dimensional topology.

Next we must make a subsequent definition for a surface on a CCC. This is that of a hyperplane. First let’s draw one on a cube:

In general, if we have a CCC then we have a hyperplane. Furthermore, if the hyperplanes are “nice" then the CCC is “special”. For the figure above the CCC is special! OK, what… But of course there is an explanation. In essence, let’s imagine a subgroup. If this subgroup has certain properties then suppose they are passed to the group itself. This is the identical concept to what we are dealing with: the hyperplane is the subgroup and the CCC is the group to which the nice properties are passed onto.
Puzzle A puzzle for the reader is to show what a self -intersecting hyperplane would like on a CC and what would a self-parallel hyperplane look like?!
We covered similar material when we talked about virtually free groups.
This begs the question, when is a CCC virtually “special”?
Suppose some group ![]() acts on a set
acts on a set ![]() and I can find subspaces permuted by
and I can find subspaces permuted by ![]() which behave like hyperplanes. Then we can produce a CCC that my group acts on. We demonstrate
which behave like hyperplanes. Then we can produce a CCC that my group acts on. We demonstrate
this claim with an example by picking some set ![]() with an accompanying cube complex. Notice, however, that this is NOT a CCC because we have a 3D cube which has non-filled in
with an accompanying cube complex. Notice, however, that this is NOT a CCC because we have a 3D cube which has non-filled in
corners — that’s not good.

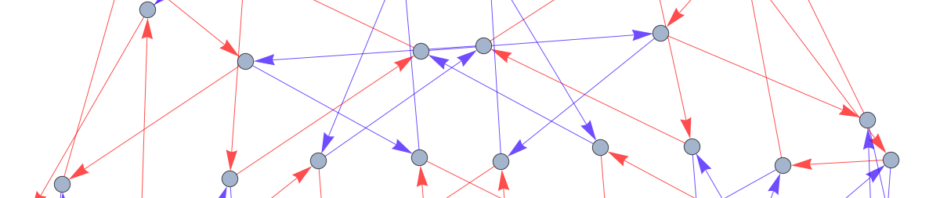
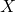 in blue and a vertex in each complimentary section is connected to neighboring ones creating a cube complex which tiles the space.
in blue and a vertex in each complimentary section is connected to neighboring ones creating a cube complex which tiles the space.
What is happening here is that we see something that looks like the corner of a cube in 2D, in this case thee squares glued together around one vertex, then we have a spot that would be a spot of positive curvature. So we must either forbid it, or fill it in with a solid 3D cube so that we have flat curvature. How do we get rid of this? We introduce orientations. For this we show another example, where we suppose 3 hyperplanes intersect to form a triangle and we put a vertex in each region. We state that we can only connect two vertices if there is a change of 1 orientation between them, where orientation is given by the arrows by the hyperplanes in the figure.
Once we have done this, our initial example can be redrawn as follows, which satisfies a CCC.

We end this short lecture with an important theorem which is somewhat of an open question with regards to precision.
Theorem When the density ![]() then CCCs are embedded trees.
then CCCs are embedded trees.

The proof, which we shall omit is done by contradiction. The general idea is provided in the figure below. In essence, we want to show that we cannot have an embedded tree on the small scale and thus we suppose we have a loop. We draw a space of two-cells which are outlined by a loop of a hyperplane. It is then possible to show that each block depicted on the loop would have to have a length of less than ![]() where
where ![]() is the isoperimetric measurement of the hyperplane for each section. The contradiction is that the box where the the hyperplane intersects itself must contribute more to the length than
is the isoperimetric measurement of the hyperplane for each section. The contradiction is that the box where the the hyperplane intersects itself must contribute more to the length than ![]() .
.
If we generalize the theorem stated on small cancellation we can use the above result to bump up the ![]() to
to ![]() .
.
Finally, it can be shown that for a group with Property T, we can never get an action on a CCC. This opens up the idea that Property T and cubulation are not allowed at the same time.
This concludes our lectures in the Geometric Group Theory seminar. It may be extremely difficult about what went down in class today. The fact is, this is state of the art mathematics, and that is itself a matter of great intrigue. What we have learned about groups acting on sets during week 1, can now be applied to a group acting on a CCC in an n-dimensional space, such as an n-dimensional sphere (whatever that means). We can now think about hyperbolic groups in ![]() -dimensions as well as the curvature that goes along with them. Although we have only went a small way into the depths, it is beautiful that we can know such a structure exists on a space we cannot even imagine.
-dimensions as well as the curvature that goes along with them. Although we have only went a small way into the depths, it is beautiful that we can know such a structure exists on a space we cannot even imagine.
Osip, I cannot lie, the last paragraph in your wonderful post made me tear up a little bit. This class truly has been a journey. A geometric, group theoretic journey. The fact is, we are really doing mathematics! We are learning about so much mathematics and solving problems and asking questions related to mathematics! When you think about it, life is really just one big path on a Cayley graph. Thank you everyone for a great class.