Motivation and Definition
When we studied free products, we discussed the free product with amalgmation very briefly. To recall, given two groups ![]() and
and ![]() , with subgroups
, with subgroups ![]() and
and ![]() and an isomorphism
and an isomorphism ![]() ; the free product of
; the free product of ![]() and
and ![]() , amalgamating the subgroups
, amalgamating the subgroups ![]() and
and ![]() by
by ![]() is the group
is the group
![]() .
.
Essentially, we are adding in a set of relators where every element of ![]() is equivalent to its image in
is equivalent to its image in ![]() . A Higman-Neumann-Neumann Extension (HNN Extension) of a group is similar, but both
. A Higman-Neumann-Neumann Extension (HNN Extension) of a group is similar, but both ![]() and
and ![]() are subgroups of the same group
are subgroups of the same group ![]() and we introduce a new, stable, generator to relate elements of
and we introduce a new, stable, generator to relate elements of ![]() to elements of
to elements of ![]() . Without further ado, let us see the definition of an HNN Extension!
. Without further ado, let us see the definition of an HNN Extension!
Definition. Let ![]() be a group with subgroups
be a group with subgroups ![]() and
and ![]() such that there exists an isomorphism
such that there exists an isomorphism ![]() from
from ![]() to
to ![]() . Then the HNN Extension of
. Then the HNN Extension of ![]() with respect to
with respect to ![]() and
and ![]() is the group
is the group
![]()
Under this definition, we retain all of the generators and relators from ![]() and add in a single stable generator,
and add in a single stable generator, ![]() . We then add in a set of relators whereby we conjugate elements of
. We then add in a set of relators whereby we conjugate elements of ![]() by
by ![]() to get their images under
to get their images under ![]() . While the definition officially requires relations for all elements of
. While the definition officially requires relations for all elements of ![]() , in practice we only need to define relators for the generators of
, in practice we only need to define relators for the generators of ![]() . Let
. Let ![]() . Then,
. Then,![]()
Since ![]() is an isomorphism, we can get the relators we need for the other elements of
is an isomorphism, we can get the relators we need for the other elements of ![]() using only the relators involving the generators.
using only the relators involving the generators.
Let us now see some examples! Let ![]() with
with ![]() and
and ![]() with
with ![]() . Then,
. Then, ![]() We will see a normal form for this group later, but for right now, we can think of words in this group as alternating between freely reduced elements of
We will see a normal form for this group later, but for right now, we can think of words in this group as alternating between freely reduced elements of ![]() and either
and either ![]() or
or ![]() , where we can reduce the word by replacing
, where we can reduce the word by replacing ![]() with
with ![]() and
and ![]() with
with ![]() .
.
Additionally, the Baumslag-Solitar groups are all HNN extensions of ![]() with
with ![]() . While we do define it here as
. While we do define it here as ![]() instead of
instead of ![]() , we can easily take
, we can easily take ![]() for
for ![]() and the presentations will be equivalent. For once they are an example and not a counter-example!
and the presentations will be equivalent. For once they are an example and not a counter-example!
Our definition and example are of an HNN Extension with a single stable letter. We can also define a more general HNN extension for a family of subgroups ![]() and a family of subgroups
and a family of subgroups ![]() with associated isomorphisms
with associated isomorphisms ![]() for each
for each ![]() pair. We would then define
pair. We would then define ![]() . However, for notational and simplification reasons we will focus the rest of this blogpost on the single stable letter case.
. However, for notational and simplification reasons we will focus the rest of this blogpost on the single stable letter case.
Britton’s Lemma
Our next goal is to define a normal form for ![]() . We will define something close to a normal form first before diving into an actual normal form. Let
. We will define something close to a normal form first before diving into an actual normal form. Let ![]() be any element of
be any element of ![]() and let
and let ![]() . Every element of
. Every element of ![]() can be written as a product
can be written as a product ![]() We will allow
We will allow ![]() to be equal to the identity in
to be equal to the identity in ![]() , so we can have higher powers of
, so we can have higher powers of ![]() if we want to but we will write them as
if we want to but we will write them as ![]() or
or ![]() . We then define a word to be reduced if and only if there is no subsequence of the form
. We then define a word to be reduced if and only if there is no subsequence of the form ![]() for
for ![]() or
or ![]() for
for ![]() . Essentially, we just reduce the word using the relators we got from the extension.
. Essentially, we just reduce the word using the relators we got from the extension.
J.L. Britton proved the following lemma:
Lemma. If the word ![]() is reduced and
is reduced and ![]() , then
, then ![]() in
in ![]() .
.
The proof of this lemma is beyond the scope of this blogpost, but can be found in “The Word Problem for Groups” by John L. Britton, published in 1958 as Lemma 4 (The Principal Lemma).
This lemma tells us that if we can reduce a word in ![]() , we can easily tell if it is equivalent to the identity, assuming that the word problem is solvable in
, we can easily tell if it is equivalent to the identity, assuming that the word problem is solvable in ![]() , so we can tell whether or not the resulting element of
, so we can tell whether or not the resulting element of ![]() is equal to the identity or not. However, there may be two words which are both reduced in
is equal to the identity or not. However, there may be two words which are both reduced in ![]() and are not equivalent, but are equal in the group. Thus, simply reducing words as described above is not enough to define a normal form. For example, consider again
and are not equivalent, but are equal in the group. Thus, simply reducing words as described above is not enough to define a normal form. For example, consider again ![]() and let
and let ![]() be
be ![]() . This is a reduced word in
. This is a reduced word in ![]() . We can, however, replace the second
. We can, however, replace the second ![]() with
with ![]() to get
to get ![]() . This word is also reduced. Instead to define a normal form, we will need to add some restrictions on what the elements of
. This word is also reduced. Instead to define a normal form, we will need to add some restrictions on what the elements of ![]() look like.
look like.
A Normal Form for HNN Extensions
As part of defining a normal form for ![]() we will choose a set of right coset representatives of both
we will choose a set of right coset representatives of both ![]() and
and ![]() and will allow
and will allow ![]() to be the representative of both
to be the representative of both ![]() and
and ![]() . We also choose a normal form for
. We also choose a normal form for ![]() We define a normal form for
We define a normal form for ![]() as follows:
as follows:
Definition. A normal form is a word ![]() for
for ![]() such that the following hold:
such that the following hold:
1. ![]() is an arbitrary element of
is an arbitrary element of ![]() in normal form,
in normal form,
2. if ![]() , then
, then ![]() is a representative of a coset of
is a representative of a coset of ![]() in
in ![]() ,
,
3. if ![]() , then
, then ![]() is a representative of a coset of
is a representative of a coset of ![]() in
in ![]() , and
, and
4. there is no consecutive sequence ![]()
we know that for all ![]() ,
, ![]() , and since
, and since ![]() is an isomorphism we can define
is an isomorphism we can define ![]() and get
and get ![]() . We can rearrange these equalities to get
. We can rearrange these equalities to get ![]() and
and ![]() We will use these relationships as we put words into their normal form. Let us consider a couple of examples.
We will use these relationships as we put words into their normal form. Let us consider a couple of examples.
Example 1.![]() ,
, ![]() Let
Let ![]() as before. We will choose the coset representatives of
as before. We will choose the coset representatives of ![]() to be the freely reduced elements of
to be the freely reduced elements of ![]() that start with a power of
that start with a power of ![]() and the coset representatives of
and the coset representatives of ![]() to be the freely reduced elements of
to be the freely reduced elements of ![]() that start with a power of
that start with a power of ![]() . Then, both 1 and
. Then, both 1 and ![]() are representative of their cosets of
are representative of their cosets of ![]() , so
, so ![]() is in normal form. However, the other word for
is in normal form. However, the other word for ![]() that we discussed before is not in normal form. Recall that we had the word
that we discussed before is not in normal form. Recall that we had the word ![]() . We know that
. We know that ![]() is not a coset representative of
is not a coset representative of ![]() , so we need to get rid of the second to last
, so we need to get rid of the second to last ![]() . We do this by using the relationship
. We do this by using the relationship ![]() , which after free reduction gives us back the sequence for
, which after free reduction gives us back the sequence for ![]() .
.
Example 2.
Let ![]() , and the coset representatives be as above. Let
, and the coset representatives be as above. Let ![]() This word is reduced, but not in a normal form as defined above. We will work right to left to put it into a normal form.
This word is reduced, but not in a normal form as defined above. We will work right to left to put it into a normal form. ![]() , and since
, and since ![]() , we need
, we need ![]() to be a representative of a coset of
to be a representative of a coset of ![]() . This is not currently the case. We use the fact that
. This is not currently the case. We use the fact that ![]() to give us
to give us ![]() Now
Now ![]() , which is in line with our definition. Next we consider
, which is in line with our definition. Next we consider ![]() and apply the same relationship to give us
and apply the same relationship to give us ![]() Applying the same idea to
Applying the same idea to ![]() gets us
gets us ![]() . Finally,
. Finally, ![]() should be a coset representative for
should be a coset representative for ![]() , which means we need to use the fact that
, which means we need to use the fact that ![]() to give us
to give us ![]() , which is finally in normal form.
, which is finally in normal form.
Normal Form Theorem for HNN Extensions
Having defined a normal form for HNN Extensions, we now prove that each of these normal forms represents a unique element in the group. This is summarized in the Normal Form Theorem for HNN Extensions:
Theorem. Let ![]() be an HNN extension. Then,
be an HNN extension. Then,
(I) The group 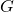 is embedded in
is embedded in 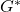 by the map
by the map 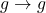 . If
. If 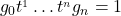 in
in 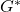 where
where 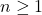 , then
, then  is not reduced.
(II) Every element
is not reduced.
(II) Every element 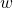 of
of 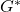 has a unique representation as
has a unique representation as 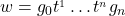 where
where  is a normal form.
is a normal form.
For the proof, we begin by showing that I implies II and vice versa so that I and II are equivalent. We do this by using Britton’s lemma and induction. We then show that statement II is actually true by defining a homomorphism from ![]() to the set of permutations of the normal forms of
to the set of permutations of the normal forms of ![]() .
.
We begin by showing that I implies II. Let ![]() be embedded in
be embedded in ![]() and assume that if
and assume that if ![]() in
in ![]() and
and ![]() , then
, then ![]() is not reduced. We wish to show that each element of
is not reduced. We wish to show that each element of ![]() has a unique normal form. Suppose that we have two normal forms for
has a unique normal form. Suppose that we have two normal forms for ![]() —
— ![]() and
and ![]() . It is enough to show that these two words are equivalent as words and not just as elements in the group. Since the two words correspond to equivalent elements we know that \begin{center}
. It is enough to show that these two words are equivalent as words and not just as elements in the group. Since the two words correspond to equivalent elements we know that \begin{center} ![]() . \end{center} If both
. \end{center} If both ![]() and
and ![]() are zero, then we have
are zero, then we have ![]() , which are both elements of
, which are both elements of ![]() and since we write the first element of any word in
and since we write the first element of any word in ![]() in normal form, we know that
in normal form, we know that ![]() and
and ![]() are the same word. Thus, suppose that
are the same word. Thus, suppose that ![]() . By rearranging the statement above, we get
. By rearranging the statement above, we get
![]() .
.
Since ![]() , we know that the number of
, we know that the number of ![]() ‘s in the sequence is at least 1, and by statement I (our assumption), this word is not reduced. However, both of our original words were reduced so the only place where there can be cancellation is in the middle. From this we know that
‘s in the sequence is at least 1, and by statement I (our assumption), this word is not reduced. However, both of our original words were reduced so the only place where there can be cancellation is in the middle. From this we know that ![]() and
and ![]() must be an element of either
must be an element of either ![]() or
or ![]() such that we can reduce. We have two cases to consider:
such that we can reduce. We have two cases to consider: ![]() and
and ![]() . Let us consider the first case first. Since
. Let us consider the first case first. Since ![]() , we know that
, we know that ![]() and
and ![]() are both coset representatives of
are both coset representatives of ![]() and are thus not elements of
and are thus not elements of ![]() . However, in order for the reduction to work, we must have that
. However, in order for the reduction to work, we must have that ![]() . The only way this works is if
. The only way this works is if ![]() . Hence,
. Hence, ![]() A similar argument holds when
A similar argument holds when ![]()
Having now shown that ![]() and
and ![]() , we can multiply on the right to get
, we can multiply on the right to get
![]() .
.
We can then follow the same process until we get to ![]() , in which case
, in which case ![]() must also equal zero for both words to be in normal form. Thus, using an inductive proof we show that
must also equal zero for both words to be in normal form. Thus, using an inductive proof we show that
![]()
not only as elements in the group but also as words, and thus, the normal form is, in fact, unique and statement II is satisfied.
Let us now assume statement II and show that statement I holds. It is clear that ![]() embeds in
embeds in ![]() by
by ![]() . We wish to show that if we have a word that represents the identity and we have at least one
. We wish to show that if we have a word that represents the identity and we have at least one ![]() in the word, then the word is not reduced. This is true by Britton’s Lemma.
in the word, then the word is not reduced. This is true by Britton’s Lemma.
Having shown that the two statements are equivalent, let us show that the theorem is in fact true. We will prove statement II. Let ![]() be the set of all normal forms and
be the set of all normal forms and ![]() and let
and let ![]() be the set of permutations of
be the set of permutations of ![]() . We define a homomorphism
. We define a homomorphism ![]() . By showing that this is in fact a homomorphism, we are showing that each element of
. By showing that this is in fact a homomorphism, we are showing that each element of ![]() permutes the normal forms in exactly one way and each of the normal forms maps to exactly one other word, so they must represent a unique element.
permutes the normal forms in exactly one way and each of the normal forms maps to exactly one other word, so they must represent a unique element.
The action of ![]() is to multiply on the left and then convert to normal form from right to left. Since we are mapping to the set of permutations, we need to always show how
is to multiply on the left and then convert to normal form from right to left. Since we are mapping to the set of permutations, we need to always show how ![]() of some element acts on a generic normal form. In order to show that it is a homomorphism, we need to define
of some element acts on a generic normal form. In order to show that it is a homomorphism, we need to define ![]() on the generators of
on the generators of ![]() (the generators of
(the generators of ![]() and
and ![]() ) and show that each of the relations under
) and show that each of the relations under ![]() still goes to 1. For any
still goes to 1. For any ![]() , we define
, we define ![]() as follows. For
as follows. For ![]() ,
, ![]() and then convert
and then convert ![]() to normal form. It is clear that
to normal form. It is clear that ![]() since we are simply multiplying on the left and can cancel out the
since we are simply multiplying on the left and can cancel out the ![]() and
and ![]() before converting to normal form.
before converting to normal form.
Let us now define ![]() . Essentially, we are still multiplying on the left and converting to normal form, but we need to carefully consider how we do it so that we end up with a normal form. If
. Essentially, we are still multiplying on the left and converting to normal form, but we need to carefully consider how we do it so that we end up with a normal form. If ![]() and
and ![]() , then once we multiply on the left we get something of the form
, then once we multiply on the left we get something of the form ![]() , which is equal to
, which is equal to ![]() . This leaves us with
. This leaves us with
![]() .
.
Otherwise, we get
![]()
which we can convert to normal form using the steps outlined in the examples to get
![]()
where ![]() and
and ![]() is the coset representative of the coset of
is the coset representative of the coset of ![]() containing
containing ![]() and
and ![]() .
.
We must also check that ![]() actually permutes the normal forms of
actually permutes the normal forms of ![]() , which we do by showing that
, which we do by showing that ![]() is a normal form. We can see that this is true because we are starting with an element of
is a normal form. We can see that this is true because we are starting with an element of ![]() , we know that
, we know that ![]() is a representative of a coset of
is a representative of a coset of ![]() and everything following was already a normal form. Finally, we need to show that
and everything following was already a normal form. Finally, we need to show that ![]() . We can verify this by considering all of the different cases (since there were two cases for
. We can verify this by considering all of the different cases (since there were two cases for ![]() ). I will not go into the details here, since this proof is already more than two pages long, but the cases are given in Lyndon and Schupp’s Combinatorial Group Theory if you are interested. Once all of the cases are considered and we have shown that the relators are still mapped to 1 under the homomorphism, we know that we have a homomorphism and then we get unique normal forms for each element.
). I will not go into the details here, since this proof is already more than two pages long, but the cases are given in Lyndon and Schupp’s Combinatorial Group Theory if you are interested. Once all of the cases are considered and we have shown that the relators are still mapped to 1 under the homomorphism, we know that we have a homomorphism and then we get unique normal forms for each element.
Conclusions
HNN extensions are important because they generate groups with interesting properties (think Baumslag-Solitar groups) and also because they are an extension of amalgamated free products. Given the Normal Form Theorem and Britton’s Lemma, we see that ![]() will have solvable word problem is everything acts “nicely” together —
will have solvable word problem is everything acts “nicely” together — ![]() has solvable word problem,
has solvable word problem, ![]() and
and ![]() have solvable word problem, and
have solvable word problem, and ![]() and
and ![]() are easily defined. HNN extensions are cool and if you want more information, look at Combinatorial Group Theory by Lyndon and Schupp!
are easily defined. HNN extensions are cool and if you want more information, look at Combinatorial Group Theory by Lyndon and Schupp!
References
Baumslag–Solitar group. (2021). In Wikipedia. \url{https://en.wikipedia.org/w/index.php?title=Baumslag%E2%80%93Solitar_group&oldid=1026392287}
Britton, J. L. (1958). The Word Problem for Groups. Proceedings of the London Mathematical Society, s3-8(4), 493–506. \url{https://doi.org/10.1112/plms/s3-8.4.493}
Britton, J. L. (1963). The Word Problem. Annals of Mathematics, 77(1), 16–32. \url{https://doi.org/10.2307/1970200}
Lyman, R. (2019, April 18). Answer to “Understanding HNN extensions: Intuition, examples, exercises.” Mathematics Stack Exchange. \url{https://math.stackexchange.com/a/3192668}
Polak, J. (2018, October 8). Britton’s lemma and a non-Hopfian fp group – Aleph Zero Categorical. \url{https://blog.jpolak.org/?p=2072}
Roger C. Lyndon and Paul E. Schupp. (2001). Higman-Neumann-Neumann Extensions and Free Products with Amalgmation. In Combinatorial Group Theory (pp. 178–186). Springer.
user1729. (2021, March 28). Answer to “Baumslag-Solitar Group.” Mathematics Stack Exchange. \url{https://math.stackexchange.com/a/4080463}