Week 2, Existence of Fundamental Domain and Some Applications

In this blog, we aim to show 1) the existence of fundamental domains, 2) fundamental domains in Cayley graphs, and 3) a one-to-one correspondence between the transversal of subgroups and components of a fundamental domain of subgroups.

1. Existence of Fundamental Domains

Last week, we introduced the notion of a fundamental domain of an action $G \curvearrowright \Gamma$ . To remind ourselves, I repeat the definition here.

Definition 1.1 If a group $G$ acts on a connected graph $\Gamma$ , then we say a subset of $\Gamma$ , denoted as $\mathcal{F}$ , is a fundamental domain of $G \curvearrowright \Gamma$ if the following three conditions are satisfied: 1) $\mathcal{F}$ is closed (in the topological sense), 2) the union $\bigcup_{g\in G} g\cdot \mathcal{F}=G$ , and 3) $\mathcal{F}$ is minimal meaning that no subsets of $\mathcal{F}$ satisfy 1) and 2).

Given this definition, we saw last week that we could construct fundamental domains of $\mathbb{Z}/6\mathbb{Z}$ on a hexagon. Indeed, fundamental domains are not unique, as we have seen from the very same example.

However, we would like to ask whether fundamental domains exist for any $G \curvearrowright \Gamma$ . At the first glance, it seems that we can naively start with some candidate $\mathcal{F}'$ such that condition 1) and 2) are satisfied. Then, we gradually shrink $\mathcal{F}'$ until the minimality condition 3) is satisfied. However, this may not work since there is no way to guarantee that the shrunk subset of $\mathcal{F}'$ is still closed.

Note that in the above example, if we start with the highlighted subset and performance the removing procedure, the minimal subset would not be closed. However, if one tries to take the closure, the minimality is not guaranteed again. There, we have to seek another way. Indeed, we state the existence of fundamental domains as a theorem. In its proof, we instead start with a minimal subgraph (warning: this is stronger than a subset!) that covers all vertices upon performing group actions, shown using Zorn’s Lemma. Then, we add some closed half-edges to cover all edges in a minimal fashion.

Theorem 1.2 If $G \curvearrowright \Gamma$ , where $\Gamma$ is connected, then there exists a fundamental domain $\mathcal{F}.$

Proof. We start by defining a poset set with minimal structure. Pick any vertex $v\in \Gamma.$ Define $P=\{\text{connected closed subgraphs of } \Gamma \mid v\in P, \text{and if } x\neq y \in P, \text{such that } g\cdot x =y \implies g=e .\}$ In other words, we would like to contain a minimal amount of vertices concerning how the group action can move things around.

Next, with the sets defined, we specify our partial order as the usual set inclusion. To use Zorn’s Lemma, we check that $P$ is nonempty since the singleton $\{v\}\in P$ . Then, we want to show that every chain has a maximal element. We assume that we have the following chain:

$\Gamma_0\subset \Gamma_1 \subset \Gamma_2 \subset \dots .$

Then, we let $\hat{\Gamma}=\bigcup \Gamma_i$ ranging over all $\Gamma_i$ in the chain. We claim that $\hat{\Gamma} \in P.$

To prove the claim, we first quickly observe that $v\in \hat{\Gamma}$ . Then, we assume that $x\neq y \in P, \text{such that } g\cdot x =y$ . There must exist $i\in \mathbb{N}$ such that $x,y\in \Gamma_i$ . Thus, by assumption, we conclude that $\hat{\Gamma} \in P.$

Therefore, we apply Zorn’s lemma to obtain a maximal element in $P$ with respect to inclusion, and we call it $\mathcal{F}'$ . We claim that $V(\bigcup g\cdot \mathcal{F}') = V(\Gamma)$ ; in other words, upon group actions, $\mathcal{F}'$ covers all vertices of $\Gamma.$

Towards a contradiction, we let $w\in V(\Gamma)$ such that $w\notin \bigcup g\cdot \mathcal{F}'$ . Thus, since $\Gamma$ is connected, there exists a vertex path from $w$ to any vertex in $\bigcup g\cdot \mathcal{F}'$ . Without loss of generality, we take the shortest path $\gamma$ . Let $w'$ be the last vertex before arriving in $\bigcup g\cdot \mathcal{F}'$ . Then, we claim that $\mathcal{F}' \cup \{w'\} \in P$ is a larger set than $\mathcal{F}'$ . To prove the claim, it suffices to show that there is no nontrivial $g\in G$ such that $g\cdot x=w'$ , which is an exact rephrase of $w'\notin \bigcup g\cdot \mathcal{F}'$ . Therefore, we have the desired contradiction.

**Diagram 1.** Illustrate that $w'$ should be contained in $\mathcal{F}'$ .

Next, we would like to extend our $\mathcal{F}'$ in a minimal fashion so that the entire graph can be covered. Here, edges are our only concerns since all vertices have been covered. Consider any edge $e$ that is not covered in $\bigcup g\cdot \mathcal{F}'$ . Observe that two endpoints of $e$ , which we call $v,w$ , should satisfy $v\in g \cdot \mathcal{F}', w\in h \cdot \mathcal{F}'$ , where $g\neq h$ . Without loss of generality, we may append the half-edge containing $v$ to $g c\dot \mathcal{F}'$ for any $e$ with endpoints $v$ and $w$ . Note that this process is equivariant up to the union of all $g \cdot \mathcal{F}'$ , so we may as well consider the extension on $e\cdot \mathcal{F}'$ , which we give the name $\mathcal{F}$ . As a quick remark here, $\mathcal{F}$ is not unique itself, which gives us the freedom to make suitable fundamental domains. (This would be a great opportunity to make some comments, like backtracking this process with the example of a hexagon.)

Finally, we check that $\mathcal{F}$ is a fundamental domain of $G \curvearrowright \Gamma$ . First, it is closed since throughout the construction, we only used unions of countably many closed subsets (I suppose we need to assume the graph $\Gamma$ is locally finite here since locally finite graphs have countably many vertices and edges on my rough inspection. But this is definitely worth commenting on.)

Second, it covers all $\Gamma$ by construction. Third, it is minimal since adding any more points on the half edges would result in repetitions equivariantly. ▭

2. Fundamental Domains of Cayley Graphs.

We can obtain many insights from the proof of Theorem 1.2. For example, we may understand the fundamental domains on different graphs. First, we introduce the following definition of vertex transitivity.

Definition 2.1 For $G$ acting on $X$ , we say that the action is (vertex)-transitive if for any $x,y\in X$ , there exists $g\in G$ such that $g\cdot x=y$ .

Remark 2.2 Groups acting on their Cayley graphs vertex-transitively. We say the underlying group is $G$ , then for any vertices $v_g,v_h$ , where $g,h\in G$ , note that $hg^{-1} \cdot v_g=v_h$ .

Then, we present a Corollary of Theorem 1.2.

Corollary 2.3 If $G$ acts on a graph transitively, then a fundamental domain of this action is a star of half edges.

Proof. We start by observing that in the construction, by fixing a vertex $v$ , any other vertex is connected through $v$ through group action. Thus, in our notation, $\mathcal{F}=\{v\}.$ Then, by attaching half-edges, we obtain a star-like fundamental domain.

Corollary 2.4 For any group acting on its Cayley group on the left, there exists a fundamental domain that’s a star of half edges.

Proof. This result trivially follows from Remark 2.2 and Corollary 2.3.

We see this corollary in action through an example.

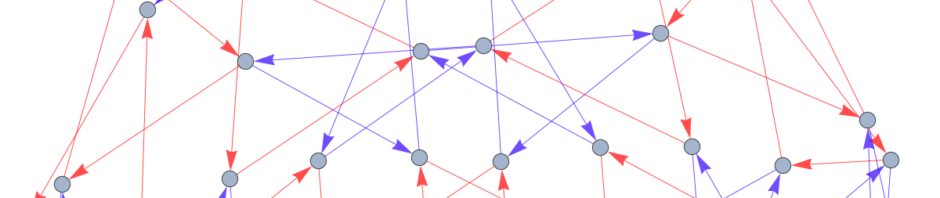
Example 2.5 We consider the Cayley graph of $S_3.$ Note that in the following picture, I draw the Cayley graph of $S_3$ generated by $\{(12), (123).\}$ Here, I denote the black color as the edges corresponding to $(1 2 3)$ and the blue color as the edges corresponding to $(1 2)$ . Then, the two red highlighted portions denote two fundamental domains of $S_3$ acting on this Cayley graph (forgetting the labels and directed edges).

3. Fundamental domains of subgroups.

In this section, my discussion will give a different treatment than what was covered in the lecture. First, we introduce the orbit and stabilizer. And then, we realize the one-to-one correspondence between the transversal of subgroups and components of a fundamental domain of subgroups as a corollary of the Orbit-Stabilizer Theorem.

Definition 3.1 Let $G$ act on $X$ . For any $x\in X$ , the stabilizer of $x$ is defined as

Stab $(x)=\{g\in G \mid g\cdot x=x.\}$

We say that an element $x\in X$ is moved freely by $G$ if the stabilizer is trivial. If every element of $X$ is moved freely, then $G$ acts freely on $X$ .

Remark 3.1′ In Diagram 1, if $x$ is in the intersections of multiple $g_i\mathcal{F}'$ , then those $g_i$ are exactly the stabilizer of the vertex $x$ .

Definition 3.2 Let $G$ act on $X$ . For any $x\in X$ , the orbit of $x$ is defined as

Orb $(x)=\{y\in X \mid y= g\cdot x.\}$

Remark 3.3 As a quick remark, in the proof of Theorem 1.2, when we define $P$ , we basically require that the subgraph does not contain any two vertices from the same orbit to obtain minimality.

Theorem 3.4 Let $G$ act on $X$ and any $x\in X$ , there is a one-to-one correspondence between the set Orb $(x)$ and left cosets of $Stab(x)$ given by $g\cdot x \to g \cdot$ Stab $(x).$

Proof. We observe that $g\cdot x=h\cdot x$ if and only if $h^{-1}g\cdot x =x \iff h^{-1}g \in \text(Stab)(x).$ Thus, two elements in the orbit are the same if and only if their induced cosets are the same.

Coming back to the picture of fundamental domains, we wish to realize this nice result when the set $X$ is a graph $\Gamma$ .

Theorem 3.5 Let $G$ act on $\Gamma$ with a fundamental domain $\mathcal{F}$ . We assume that no group action fixes $\mathcal{F}$ nontrivially. Then, if $H$ is a subgroup of $G$ and a fundamental domain of $H$ is a union of $n$ copies of $\mathcal{F}$ (where $n$ can also be infinity), the index of $H$ in $G$ is $n.$

Proof. Since no group action fixes $\mathcal{F}$ nontrivially, we deduce that there is some point in $\mathcal{F}$ that is moved freely by $G$ . Therefore, we have a bijection between elements of $G$ and points in Orb $(x)$ . By assumption, we note that

$\mathcal{F}_H=\bigcup_{i=1}^n g_i \mathcal{F},$ where $n$ can also take on infinity.

Since $\mathcal{F}_H$ is a fundamental domain for the action $H$ , we can deduce $g\cdot x=g_ih\cdot x$ for one of the $g_i$ mentioned above. Using Theorem 3.4 to come back to the group side, we conclude that $\{g_i\}$ forms a transversal of $H$ in $G$ . Hence, we prove the theorem.

10 Responses to Week 2, Existence of Fundamental Domain and Some Applications

Osip Surdutovich says:

September 23, 2022 at 12:38 am

Shuhang! Great post!! I really liked how you laid out all the definitions and theorems we covered in class in a very logical and clear way. One thing I am still a bit confused about is the proof of Corollary 2.3, how do we know it is always a star of half edges? It seems very surprising to me that this is true but I think I’m just having trouble wrapping my head around it. I’ll work through it another time and do some examples and it might make more sense though.
Overall, amazing work!

- Shuhang Xue says:
  
  September 25, 2022 at 2:33 am
  
  In my understanding, its because that in the construction, we want a set of vertices that does not include any two verticies such that the group action on one will result in the other one. However, if a group acts transitively on a graph. Then by definition, you cannot include any other vertex but the one you started with. Then, you can add edges to complete the construction to see it is star-shaped.
  
Horace Fusco says:

September 24, 2022 at 6:26 pm

Nice work! I really appreciated how you made a connection with the orbit-stabilizer relationship. I got a little lost in the proof of theorem 3.5 though. I think maybe the root of my confusion is that I’m not completely clear on what it means for no group action to fix the fundamental domain nontrivially. Could explain what you mean by that?

- Shuhang Xue says:
  
  October 1, 2022 at 5:36 pm
  
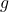  Sorry about the late reply. I meant that if $g\cdot \mathcal{F}=\mathcal{F}$ , then $g$ has to be the identity element. Notice that I need this assumption to say that at least there is one point in $\mathcal{F}$ that is movedly freely by $G$ . This point is needed in the proof to apply the orbit-stabilizer relation.
  
Akash Ganguly says:

September 25, 2022 at 9:57 pm

Shuhang. What a beautiful post. I’ve had little experience with Zorn’s lemma and was a little confused about the parts where you used it. Could you point me towards any resources or maybe just a few lines of intuition that helped you think about it?

- Shuhang Xue says:
  
  September 26, 2022 at 2:29 pm
  
  Thank you! I state Zorn’s Lemma in the following language of postes.
  Suppose we have a nonempty partially ordered set P. If every nonempty chain has an upper bound in P, then we have a maximal element on P.
  
  I would encourage you to use this to prove some simple statements:
  1. every vector space has a basis.
  2. every nonempty ring with unity has a maximal ideal.
  
  Indeed, I recall that Zorn’s lemma is equivalent to the Axiom of Choice, which may be an interesting exercise for folks. As for reference, I just learned it in algebra. Also, Wikipedia page might have decent enough information.
  
Michaela Polley says:

September 25, 2022 at 10:08 pm

Nice post, Shuhang! I am still confused by the proof of Theorem 1.2. What exactly is the poset that you defined as $P$ ? How are we actually constructing it? I understand that $v\in P$ . One of our conditions on $P$ is that $v\in P$ . Does the $P$ here refer to an element of the larger set $P$ ?

Additionally, how are we showing that $\hat{\Gamma}\in P$ ? It is clear that it contains v, but how do we show the second condition? Any clarification would be appreciated!

- Shuhang Xue says:
  
  September 26, 2022 at 2:33 pm
  
  Thank you. The poset consists of sets of vertices such that none will result in a distinct vertex upon a group action. Then, the partial relation here is just set inclusion. Therefore, it should be $\{v\} \in P$ . Sorry if I had some typos.
  
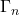  As for the second question, we start with two arbitrary verticies $v,w$ . Then, by construction, they both live in a specific $\Gamma_n$ . Therefore, we can use our assumption on 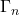$\Gamma_n$ to conclude that the second condition is satisfied.
  
John Eichelberger says:

September 26, 2022 at 3:29 pm

Awesome post! One thing your discussion of Fundamental Domains makes me think about is what an efficient Fundamental Domain generating algorithm might look like. You could certainly brute-force it by computing the behavior of every vertex and edge over every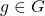 $g \in G$ , and I’m not sure that in a general case you can be substantially faster than that. However, I’d be curious to know how computability changes based on the graph and the acting group.

- MurphyKate says:
  
  September 30, 2022 at 11:11 pm
  
  That’s a great question, John. I don’t know the answer, but it reminds me of questions around automaticity of groups, which we will (hopefully) get to later in the term! If you’re interested, you could check out the book Word Processing in Groups from the library.