Wednesday’s class was a review of groups, a “whirlwind-review” of the basics of graphs and trees, and a look at actions on symmetry groups of geometric object.
Groups, Reviewed
To begin with, we reviewed group presentations, of form ![]() . For instance, the integers over addition can be conceived of as
. For instance, the integers over addition can be conceived of as
![]()
In particular, we note that exponentiation works as expected, where exponentiation represents addition:
![]()
What is “the” representation of \mathbb{Z} \times \mathbb{Z}? In short, it depends; there are infinitely many valid representations. For instance,
However, while these are all representations of the same group, we cannot just “simplify” one into another. It’s true that generators are analogous to a basis in linear algebra, in the sense that groups are constructed by combinations of generators just as a vector space is constructed from its constituent vectors. But the analogy is strained when it comes to a “minimal basis”. Consider the following example:
![]()
These both represent the same group; the first has three generators, and the second only has one. Yet in both cases the removal of any generator means we no longer have the same group.
This warm-up leads us to several key, enduring questions across geometric group theory:
- For a group
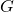 , is
, is 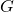 finitely presented? Is it finitely generated?
finitely presented? Is it finitely generated? - When is a presentation trivial? Given a presentation, when does it represent
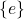 ?
? - Given a word
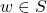 , does
, does  ?
?
Group Actions
Definition. A group ![]() acts on a set
acts on a set ![]() where for every
where for every ![]() ,
,
![]()
with the following properties satisfied:
We want to think about this definition in a deeper way, thinking about symmetry. So for an object ![]() , consider Sym
, consider Sym![]() , the group of symmetries on
, the group of symmetries on ![]() . (This is often referred to as Aut
. (This is often referred to as Aut![]() , the automorphisms on
, the automorphisms on ![]() .) We can think of
.) We can think of ![]() acting on
acting on ![]() as a homomorphism
as a homomorphism
![]()
In other words, we want to assign the behaviors of elements of ![]() to the behaviors the groups that arise in
to the behaviors the groups that arise in ![]() .
.
We have a faithful group action if ![]() is injective. Equivalently,
is injective. Equivalently, ![]() acts faithfully if
acts faithfully if ![]() implies that there is some
implies that there is some ![]() such that
such that ![]() , or in other words, that every non-identity element of
, or in other words, that every non-identity element of ![]() does something to some element of
does something to some element of ![]() under the action. For an example of a faithful action, consider actions on a square, letting
under the action. For an example of a faithful action, consider actions on a square, letting ![]() . We define the action as
. We define the action as ![]() . This action is faithful, because every non-identity
. This action is faithful, because every non-identity ![]() will permute the corners of the square.
will permute the corners of the square.
For an example of an action that is not faithful, we’ll consider the trivial case: for any ![]() and any
and any ![]() acting on
acting on ![]() , we can define the action by
, we can define the action by ![]() . In other words, every configuration of
. In other words, every configuration of ![]() maps to itself under every action of
maps to itself under every action of ![]() .
.
Theorem. Every group ![]() can be faithfully represented by a group action on the symmetries of an object
can be faithfully represented by a group action on the symmetries of an object ![]() .
.
Proof. Let the object ![]() be given by the set of elements of
be given by the set of elements of ![]() . We’ll define our action
. We’ll define our action ![]() as the multiplication operator of
as the multiplication operator of ![]() , which is to say
, which is to say ![]() . This action will be associative because
. This action will be associative because ![]() , and because
, and because ![]() is (also) a group, elements under its operator associate; it likewise follows that our action will have an identity, since
is (also) a group, elements under its operator associate; it likewise follows that our action will have an identity, since ![]() is a group. Finally, consider some
is a group. Finally, consider some ![]() , and let
, and let ![]() . We have that
. We have that ![]() , so for every
, so for every ![]() there is some
there is some ![]() such that
such that ![]() , as desired.
, as desired.
The following corollary serves as a generalization of Cayley’s Theorem from Abstract I, that every finite group is a subgroup of a symmetric group.
Corollary. ![]() for some
for some ![]() .
.
Proof. It follows from the above theorem that ![]() is injective. Thus
is injective. Thus
![]()
A Whirlwind of Graph Theory
The following are some foundational definitions for graph theory.
Definition. A graph ![]() is a set containing
is a set containing
![]() , a set of vertices,
, a set of vertices,
![]() , a multiset of edges
, a multiset of edges
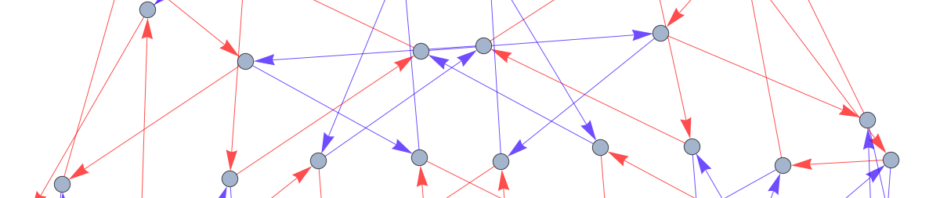
Below is an example graph ![]() .
.

Definition. A path is a collection of edges and vertices that begins and ends with a vertex, with each edge connected to the previous vertex.
Note. The length of a path is given by the number of edges.
Definition. A path with the same initial and final vertex is a cycle.
Definition. A path is considered reduced if it contains no backtracks.
Definition. A graph is considered connected if there exists a path between any pair of vertices.
Definition. A graph is considered finite if ![]() and
and ![]() are finite.
are finite.
Definition. A graph is considered locally finite if deg![]() is finite for all
is finite for all ![]() .
.
Definition. A tree is a connected graph with no cycles.
Note. We denote ![]() as the regular tree, given by a tree where every vertex connects to
as the regular tree, given by a tree where every vertex connects to ![]() edges. Similarly,
edges. Similarly, ![]() refers to a tree in which every vertex has either
refers to a tree in which every vertex has either ![]() or
or ![]() vertices.
vertices.
Theorem. The following are equivalent:
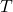 is a tree.
is a tree.- There exists a unique reduced path for all
 .
. - For all
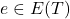 ,
, 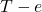 is disconnected.
is disconnected.
These can be shown to follow by contradiction.
Symmetries on Graphs
With this setup, we can consider actions on graphs! Similar to rigid symmetries, we require that a symmetry ![]() must be a bijective map of edges and vertices, and that
must be a bijective map of edges and vertices, and that ![]() must preserve some sense of structure in the graph, what MurphyKate calls “preserving gluing.”
must preserve some sense of structure in the graph, what MurphyKate calls “preserving gluing.”
To get a sense for what this means, consider two graphs. ![]() is the graph of four points, each connected to every other point by an edge.
is the graph of four points, each connected to every other point by an edge.
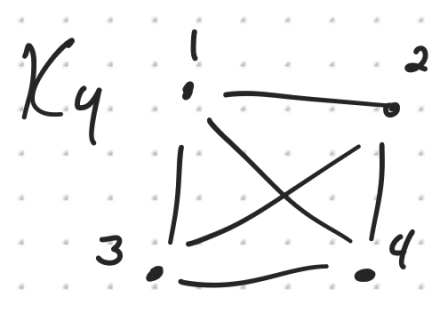
By numbering the points, we see that we can swap any pair of points as we please and preserve the shape of the graph. Therefore the group of symmetries on ![]() is isomorphic to
is isomorphic to ![]() , the symmetries on four elements.
, the symmetries on four elements.
On the other hand, consider the graph ![]() .
.

If we swapped 1 and 4, we would lose the property of “gluedness”. Similarly, we aren’t allowed to swap 2 and 4. Therefore we have that Sym![]() . It turns out that Sym
. It turns out that Sym![]() , with its four points and four edges, is isomorphic to
, with its four points and four edges, is isomorphic to ![]() , the rigid symmetries of a square.
, the rigid symmetries of a square.
But we can kick it up a notch with multiedges. The colors in ![]() below mark where each part of its symmetry group come fromm and are not considered decorations:
below mark where each part of its symmetry group come fromm and are not considered decorations:

But we can kick it up another notch with digraphs!
Definition. A directed graph (aka digraph) is a graph where every edge has an orientation toward a vertex. For instance:

That example has only one symmetry, formed by swapping the left and right multiedges. But we can kick it up again with colors! We can color every edge:

This example has only the trivial symmetry. So when considering a graph, we can consider separately Sym![]() , as previously established, and Sym
, as previously established, and Sym![]() , the symmetry group that preserves orientation and color.
, the symmetry group that preserves orientation and color.
Theorem. For any graph ![]() , Sym
, Sym![]() .
.
Proof. Left as an exercise. <3
And weighing in at five pages in Google docs, that wraps up my notes. Friday we’ll talk about Cayley graphs, and if I’m reading the textbook chapter headers correctly, the topic of group actions on the symmetry groups of graphs will last us most of the term.
Yay graph theory! 🙂
Great write-up John! You give a very nice review of group actions and introduction to graphs. Interestingly, some of the terminology we used on Wednesday for graph-related concepts differs from what I’ve seen in combinatorics / theoretical CS contexts. For instance, most definitions of “path” I’ve seen have specified that a path does not permit repeated vertices (while a path with repeated vertices and edges might be considered a “walk”). It’s interesting that GGT would have a different approach to defining this term. I wonder if there’s some algebraic reason it’s more convenient to allow for repeated vertices and edges.
Great question! My quick answer is that it depends on the specifics of your definition. We’re trying to define it combinatorially here, so we’ll allow “repeated edges” as long as you start going one direction along the edge and then go the other direction. We don’t allow repeated vertices (note that the definition requires that we alternative vertex and edges). It is OK to cover some vertex twice – if this is disallowed in CS it’s probably because it’s inefficient! (Though you might want to chat with your CS prof about this).
This is a really interesting explanation. It’s true that algorithmists and complexity theorists are usually interested in problems regarding paths without repeated vertices, as they arise naturally in optimization contexts. Several classic NP-hard problems are also related to paths without repeated vertices (see: the Hamiltonian Path problem), while analogous problems on paths with repeated vertices are easy to compute (see: Eulerian trails). In a vague sense, problems related to paths require more knowledge about the structure of the underlying graph when they require that the path contain each vertex at most once.
Additionally, statements that assume the existence of a path between two vertices can be made with the more restrictive definition (example: “a graph is connected if there exists a path between any pair of vertices”). Moreover, graph theorists may want to study paths without repeated vertices because such a path can itself be considered a subgraph of the larger graph. This allows one to define some interesting notions (see: pathwidth) that conceive of paths as a class of graphs, rather than a sequence of vertices and edges.
Nice blog post! I realized as I read it that I’ve been visualizing group actions in terms of graph theory almost subconsciously. For example, when I think about the symmetries of a square, I’ve been seeing the square as a planar graph, and separating all of the edges and vertices and rearranging them.
My first introduction to group actions was in the context of . The ‘boolean algebra of rank 3’ was defined as the set B3 = {{123},{12},{13},{23},{1},{2},{3},{}}. (the last one being the empty set). It’s the combinations of 3 objects. I then looked for orbits of the action of the transposition (12). The action would send {1} to {2}, and {2} back to {1} forming one orbit. {13} and {23} are a similar case, and we consider {12} and {21} to be the same in this context. Finally, we end up with the orbits [{123}],[{12}],[{13},{23}],[{3}],[{1},{2}],[{}]. This then led to a ‘quotient poset’ where elements of the same orbit are considered the same element. These can be represented more visually through a Hasse diagram, but I can’t figure out how to add images to these comments so please shoot me a message if you’d like to see them!
I agree, the idea of orbitals as an actual *path* was how I originally conceptualized the idea of being able to have a subset of states you can reach from a given starting point in a group. I have very little background in graph theory, and it’s been satisfying to see that this vague understanding of structure can be modeled precisely.
And yes, Hasse diagrams are awesome!
I give a comment on the usage of Symmetric Group in the post and also in the textbook. The common symmetric groups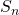 we are in love with are a special case of a general symmetric structure. The notation of my discussion is based on our textbook.
we are in love with are a special case of a general symmetric structure. The notation of my discussion is based on our textbook.
Indeed, we can consider an arbitrary mathematical object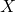 . It can be a regular n-gon, a finite set, or even a vector space. Then, we can define the SYM(X) as the set of all bijections from
. It can be a regular n-gon, a finite set, or even a vector space. Then, we can define the SYM(X) as the set of all bijections from  to
to 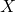 that preserves the underlying structure of the object. Under such a general context, we note that SYM(n-gon) is the dihedral group
that preserves the underlying structure of the object. Under such a general context, we note that SYM(n-gon) is the dihedral group 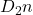 ; SYM(
; SYM( ) is
) is 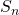 ; and SYM(
; and SYM( ), where
), where  is a vector space, is the group of all linear operators.
is a vector space, is the group of all linear operators.
With this machinery, we can make sense of John’s discussion of Cayley’s Theorem. Indeed, we view the symmetric group of a group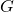 as a subgroup of the symmetric group of the underlying set structure, namely
as a subgroup of the symmetric group of the underlying set structure, namely 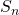 , where
, where 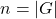 . Thus, by the transitivity of subgroups, any group is realized as a subgroup of symmetric groups through an action induced by the multiplication of the group. This is a beautiful theorem since it reassures our intuition about groups, a well-orchestrated set structure –– groups are symmetric objects that are always realizable through permutations.
. Thus, by the transitivity of subgroups, any group is realized as a subgroup of symmetric groups through an action induced by the multiplication of the group. This is a beautiful theorem since it reassures our intuition about groups, a well-orchestrated set structure –– groups are symmetric objects that are always realizable through permutations.
Shuhang Xue
I also want to discuss the graphs of our interest in the textbook. Indeed, we view graphs topologically. In concrete terms, we see graphs as CW-complexes with only zero and one cells, which is standardly denoted as each homeomorphic to
each homeomorphic to  the
the 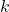 -dimensional disk, where
-dimensional disk, where 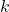 denotes the dimension and
denotes the dimension and 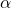 denotes the index of cells. This construction builds topological spaces iteratively at each level
denotes the index of cells. This construction builds topological spaces iteratively at each level 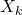 by specifying gluing maps
by specifying gluing maps 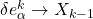 . We call each
. We call each 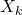 as the
as the 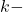 skeleton. With those
skeleton. With those  , we can define
, we can define 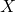 to be their direct limit with weak topology to define a CW-complex.
to be their direct limit with weak topology to define a CW-complex.
The above discussion may seem technical. But the takeaway is that we view graphs topologically. For folks interested in algebraic topology, I am happy to discuss the definition of CW-complexes in further detail 🙂
Very thorough and impressive post! I really appreciated your description about the symmetries of a graph. I think it’s nice the way you built up the discussion by beginning with the bare graph and then extending to symmetries that also preserve decorations. One note on the example graph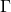 is that I believe there is a symmetry that swaps vertices
is that I believe there is a symmetry that swaps vertices 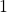 ad
ad 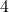 and fixes
and fixes 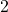 and
and  since the former two vertices have the same neighbors. Though swapping
since the former two vertices have the same neighbors. Though swapping 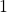 and
and 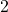 while fixing
while fixing  and
and 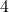 would be a problem.
would be a problem.
I also liked your illustrations a lot. Having diagrams with color is priceless–maybe some time you can show me how you make those because I haven’t had a ton of success with that in the past.
Thanks! I mostly followed the structure of the lecture — it was helpful to start with simple graphs and work our way up. Yes, you’re right about the mistake on the symmetries of the square, a diagonal reflection would swap 1 and 4 while fixing 2 and 3, the correct non-symmetry is what you mentioned.
I take my notes on a tablet — one of the big motivators for getting one was being able to quickly switch colors!
Nice post! Quick formatting note — in the third paragraph under “Groups, reviewed” you forgot to go into math mode, so some of the LaTeX didn’t format correctly. Not a big deal, just letting you know.
I’m still a little bit confused about group actions and the symmetric group for a given set X. Here’s my current understanding: The symmetries of a set X are a subset of configurations of the elements of X. I believe that this is a subset of the automorphisms of X, but am not sure. These symmetries all preserve some feature of the set X that we care about (like “gluing”). Then, a group action comes into play somehow? I think this is where I am getting lost… Any advice would be appreciated!
In your notation, I think that the symmetries of a *set* X are exactly all of the possible permutations of the elements of X. So Sym(X) = Aut(X). If we want to add in some more structure (so perhaps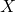 is no longer just a set, but a graph, or a labelled graph), we talk about
is no longer just a set, but a graph, or a labelled graph), we talk about 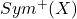 . This will be a subgroup of
. This will be a subgroup of 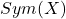 .
.
Great post! I really like the whirlwind section where you list the definitions. They are really clear and when I’ll be doing homework I will use this as a quick reference table to check what we can do! Also the figures are really neat and make a lot of sense!